Linear Programming

Sumber Gambar: people.richland.edu

Linear Programming atau Pemrograman Linier disingkat PL merupakan metode matematik dalam mengalokasikan sumber daya yang terbatas untuk mencapai suatu tujuan seperti memaksimumkan keuntungan dan meminimumkan biaya. PL banyak diterapkan dalam masalah ekonomi, industri, militer, social dan lain-lain. PL berkaitan dengan penjelasan suatu kasus dalam dunia nyata sebagai suatu model matematik yang terdiri dari sebuah fungsi tujuan linier dengan beberapa kendala linier (Siringoringo, 2005).

Menurut Media Anugerah Ayu (1996), linear programming atau pemrograman linier berasal dari kata pemrograman dan linear. Pemograman artinya perencanaan, dan linear berarti bahwa fungsi-fungsi yang digunakan merupakan fungsi linier. Jadi secara umum linear programming adalah suatu teknik perencanaan yang bersifat analitis yang analisisnya memakai model matematika, dengan tujuan menemukan beberapa kombinasi alternatif pemecahan masalah, yang kemudian dipilih yang terbaik yang diantaranya dalam rangka menyusun langkah-langkah kebijaksanaan lebih lanjut tentang alokasi sumber daya dan dana yang terbatas guna mencapai tujuan dan sasaran yang diinginkan secara optimal.

Sedangkan menurut Wikipedia (2009), Linear Programming merupakan suatu model umum yang dapat digunakan dalam pengalokasian sumber-sumber yang terbatas secara optimal. Masalah tersebut timbul apabila seseorang diharuskan untuk memilih atau menentukan tingkat setiap kegiatan yang akan dilakukan, dimana masing-masing kegiatan membutuhkan sumber yang sama sedangkan jumlahnya terbatas.

Karakteristik yang biasa digunakan dalam persoalan linear programming adalah sebagai berikut (Siringoringo, 2005):

1. Sifat linearitas suatu kasus dapat ditentukan dengan menggunakan beberapa cara. Secara statistik, kita dapat memeriksa kelinearan menggunakan grafik (diagram pencar) ataupun menggunakan uji hipotesa. Secara teknis, linearitas ditunjukkan oleh adanya sifat proporsionalitas, additivitas, divisibilitas dan kepastian fungsi tujuan dan pembatas.

2. Sifat proporsional dipenuhi jika kontribusi setiap variabel pada fungsi tujuan atau penggunaan sumber daya yang membatasi proporsional terhadap level nilai variabel. Jika harga per unit produk misalnya adalah sama berapapun jumlah yang dibeli, maka sifat proporsional dipenuhi. Atau dengan kata lain, jika pembelian dalam jumlah besar mendapatkan diskon, maka sifat proporsional tidak dipenuhi. Jika penggunaan sumber daya per unitnya tergantung dari jumlah yang diproduksi, maka sifat proporsionalitas tidak dipenuhi.

3. Sifat additivitas mengasumsikan bahwa tidak ada bentuk perkalian silang diantara berbagai aktivitas, sehingga tidak akan ditemukan bentuk perkalian silang pada model. Sifat additivitas berlaku baik bagi fungsi tujuan maupun pembatas (kendala). Sifat additivitas dipenuhi jika fungsi tujuan merupakan penambahan langsung kontribusi masing-masing variabel keputusan. Untuk fungsi kendala, sifat additivitas dipenuhi jika nilai kanan merupakan total penggunaaan masing-masing variabel keputusan. Jika dua variabel keputusan misalnya merepresentasikan dua produk substitusi, dimana peningkatan volume penjualan salah satu produk akan mengurangi volume penjualan produk lainnya dalam pasar yang sama, maka sifat additivitas tidak terpenuhi.

4. Sifat divisibilitas berarti unit aktivitas dapat dibagi ke dalam sembarang level fraksional, sehingga nilai variabel keputusan non integer dimungkinkan.

5. Sifat kepastian menunjukkan bahwa semua parameter model berupa konstanta. Artinya koefisien fungsi tujuan maupun fungsi pembatas merupakan suatu nilai pasti, bukan merupakan nilai dengan peluang tertentu.

Keempat asumsi (sifat) karakteristik ini dalam dunia nyata tidak selalu dapat dipenuhi. Untuk meyakinkan dipenuhinya keempat asumsi ini, dalam linear programming diperlukan analisis sensitivitas terhadap solusi optimal yang diperoleh.

-->

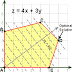
Penyelesaian dengan Metode Grafik

Metode grafik adalah penyelesaian linear programming yang penyelesaiannya disajikan dalam bentuk grafik yang sebelumnya dilakukan perhitungan-perhitungan untuk mencari titik-titik temu pada masing-masing sumbu. Tujuan dari metode grafik ini adalah untuk memberi dasar-dasar dari konsep yang digunakan teknik simpleks. Prosedur umumnya adalah untuk mengubah suatu situasi deksriptif kedalam bentuk masalah linear programming dengan menentukan variabel, konstanta, fungsi objektif, dan kendalanya sehingga masalah tersebut dapat disajikan dalam bentuk grafik dan diinterpretasikan solusinya (Dimyati, 1994).

Metode grafik hanya bisa digunakan untuk menyelesaikan permasalahan dimana hanya terdapat dua variabel keputusan. Untuk menyelesaikan permasalahan tersebut, langkah pertama yang harus dilakukan adalah memformulasikan permasalahan yang ada ke dalam bentuk linear programming (Dimyati, 1994).

Langkah-langkah dalam formulasi permasalahan adalah (Dimyati, 1994):

1. Pahamilah secara menyeluruh permasalahan manajerial yang dihadapi.

2. Identifikasikan tujuan dan kendalanya.

3. Definisikan variabel keputusannya.

4. Gunakan variabel keputusan untuk merumuskan fungsi tujuan dan fungsi kendala secara matematis.

Berikut adalah tahapan-tahapan dalam penggunaan metode grafik (Dimyati, 1994):

1. Identifikasi variabel keputusan.

2. Identifikasi fungsi objektif.

3.Identifikasi kendala-kendala.

4. Menggambarkan bentuk grafik dari semua kendala.

5. Identifikasi daerah solusi yang layak pada grafik.

6. Menggambarkan bentuk grafik dari fugsi objektif dan menentukan titik yang memberikan nilai objektif optimal pada daerah solusi yang layak.

7.Mengartikan solusi yang diperoleh.

Penyelesaian dengan Metode Simpleks

Salah satu teknik penentuan solusi optimal yang digunakan dalam linear programming adalah metode simpleks. Penentuan solusi optimal menggunakan metode simpleks didasarkan pada teknik eleminasi Gauss Jordan. Penentuan solusi optimal dilakukan dengan memeriksa titik ekstrim satu per satu dengan cara perhitungan iteratif. Sehingga penentuan solusi optimal dengan simpleks dilakukan tahap demi tahap yang disebut dengan iterasi. Iterasi ke-i hanya tergantung dari iterasi sebelumnya (i-1) (Siringoringo, 2005).

Ada beberapa istilah yang sangat sering digunakan dalam metode simpleks, diantaranya (Siringoringo, 2005):

1. Iterasi adalah tahapan perhitungan dimana nilai dalam perhitungan itu tergantung dari nilai tabel sebelumnya.

2. Variabel non basis adalah variabel yang nilainya diatur menjadi nol pada sembarang iterasi. Dalam terminologi umum, jumlah variabel non basis selalu sama dengan derajat bebas dalam sistem persamaan.

3. Variabel basis merupakan variabel yang nilainya bukan nol pada sembarang iterasi. Pada solusi awal, variabel basis merupakan variabel slack (jika fungsi kendala merupakan pertidaksamaan ≤) atau variabel buatan (jika fungsi kendala menggunakan pertidaksamaan ≥ atau =). Secara umum, jumlah variabel basis selalu sama dengan jumlah fungsi pembatas (tanpa fungsi non negatif).

4. Solusi atau nilai kanan merupakan nilai sumber daya pembatas yang masih tersedia. Pada solusi awal, nilai kanan atau solusi sama dengan jumlah sumber daya pembatas awal yang ada, karena aktivitas belum dilaksanakan.

5. Variabel slack adalah variabel yang ditambahkan ke model matematik kendala untuk mengkonversikan pertidaksamaan (≤) menjadi persamaan (=). Penambahan variabel ini terjadi pada tahap inisialisasi. Pada solusi awal, variabel slack akan berfungsi sebagai variabel basis.

6. Variabel surplus adalah variabel yang dikurangkan dari model matematik kendala untuk mengkonversikan pertidaksamaan ≥ menjadi persamaan (=). Penambahan ini terjadi pada tahap inisialisasi. Pada solusi awal, variabel surplus tidak dapat berfungsi sebagai variabel basis.

7. Variabel buatan adalah variabel yang ditambahkan ke model matematik kendala dengan bentuk (≥) atau (=) untuk difungsikan sebagai variabel basis awal. Penambahan variabel ini terjadi pada tahap inisialisasi. Variabel ini harus bernilai 0 pada solusi optimal, karena kenyataannya variabel ini tidak ada. Variabel hanya ada di atas kertas.

8. Kolom pivot (kolom kerja) adalah kolom yang memuat variabel masuk. Koefisien pada kolom ini akn menjadi pembagi nilai kanan untuk menentukan baris pivot (baris kerja).

9. Baris pivot (baris kerja) adalah salah satu baris dari antara variabel basis yang memuat variabel keluar.

10. Elemen pivot (elemen kerja) adalah elemen yang terletak pada perpotongan kolom dan baris pivot. Elemen pivot akan menjadi dasar perhitungan untuk tabel simpleks berikutnya.

11. Variabel masuk adalah variabel yang terpilih untuk menjadi variabel basis pada iterasi berikutnya. Variabel masuk dipilih satu dari antara variabel non basis pada setiap iterasi. Variabel ini pada iterasi berikutnya akan bernilai positif.

12. Variabel keluar adalah variabel yang keluar dari variabel basis pada iterasi berikutnya dan digantikan oleh variabel masuk. Variabel keluar dipilih satu dari antara variabel basis pada setiap iiterasi. Variabel ini pada iterasi berikutnya akan bernilai nol.

Sebelum melakukan perhitungan iteratif untuk menentukan solusi optimal, pertama sekali bentuk umum linear programming dirubah ke dalam bentuk baku terlebih dahulu. Bentuk baku dalam metode simpleks tidak hanya mengubah persamaan kendala ke dalam bentuk sama dengan, tetapi setiap fungsi kendala harus diwakili oleh satu variabel basis awal. Variabel basis awal menunjukkan status sumber daya pada kondisi sebelum ada aktivitas yang dilakukan. Dengan kata lain, variabel keputusan semuanya masih bernilai nol. Dengan demikian, meskipun fungsi kendala pada bentuk umum linear programming sudah dalam bentuk persamaan, fungsi kendala tersebut masih harus tetap berubah (Siringoringo, 2005).